Blog Post

Neural Graphics: From First Principles to Performance

---

In my last blog post, I gave an introduction to how gradient descent is used to drive gaussian splatting representations– essentially, going through a list of blobs in 2D space, calculating their color values at a specific texture coordinate, and blending them together, and iteratively adjusting them to be as close as possible to an ideal target image. Notably, this simplified version had significant performance and quality limitations. In this post, I’ll take you through the changes needed to go from that simple pedagogical example to an implementation that achieves real-time performance.

A More Efficient Algorithm

The key limitation of our previous implementation was that it evaluated every gaussian blob for every pixel. This is extremely inefficient since most gaussians only affect a small region of pixels. We can do much better by breaking this into three logical steps:

1. For each gaussian, determine which tiles of the image it will affect (coarse rasterization)
2. For each tile, sort its affecting gaussians back-to-front
3. For each pixel in the tile, accumulate the color contributions only from gaussians that affect that tile (fine rasterization)

While we could implement these as separate compute kernels, we can achieve better performance by combining them into a single kernel using workgroup-level collaboration between threads. Let’s look at how this works.

Tile-based Rasterization with Workgroups

The core optimization in our approach is to divide the image into tiles, where each tile is processed by a compute workgroup - a collection of threads that execute together and can share data efficiently. This allows us to:

1. Build a per-tile shortlist of only the gaussians that affect that tile
2. Sort just those gaussians that affect the tile
3. Process pixels within the tile using only the relevant gaussians

A workgroup is a collection of threads that execute simultaneously on the same compute unit. These threads can collaborate using special operations and share data quickly through a small amount of on-chip memory. We’ll use this capability to efficiently build and process our per-tile gaussian lists.

Here’s how the implementation works in Slang:

// ----- Constants and definitions --------

static const int GAUSSIANS_PER_BLOCK = 512;
static const int WG_X = 8;
static const int WG_Y = 4;

// -----------------------------------------

// Some types to hold state info on the 'blobs' buffer.
// This makes it easy to make sure we're not accidentally using the buffer
// in the wrong state.
//
// The actual data is in the 'blobs' object.
//
struct InitializedShortList { int _dummy = 0; };
struct FilledShortList { int _dummy = 0; };
struct PaddedShortList { int _dummy = 0; };
struct SortedShortList { int _dummy = 0; };

/*
 * coarseRasterize() calculates a subset of blobs that intersect with the current tile. Expects the blob counters to be reset before calling.
 *
 * The coarse rasterization step determines a subset of blobs that intersect with the tile.
 * Each thread in the workgroup takes a subset of blobs and uses bounding-box intersection tests to determine
 * if the tile associated with this workgroup overlaps with the blob's bounds.
 *
 * Note: This is a simplistic implementation, so there is a limit to the number of blobs in the short-list (NUM_GAUSSIANS_PER_BLOCK).
 * In practice, if the number of blobs per tile exceeds this, NUM_GAUSSIANS_PER_BLOCK must be increased manually.
 * A more sophisticated implementation would perform multiple passes to handle this case.
 *
 */
FilledShortList coarseRasterize(InitializedShortList sList, Blobs blobset, OBB tileBounds, uint localIdx)
{
    GroupMemoryBarrierWithGroupSync();

    Gaussian2D gaussian;
    uint numGaussians = Gaussian2D.count(blobset);
    for (uint i = localIdx; i < numGaussians; i += (WG_X * WG_Y))
    {
        gaussian = Gaussian2D.load(blobset, i, localIdx);
        OBB bounds = gaussian.bounds();
        if (bounds.intersects(tileBounds))
        {
            blobs[blobCountAT++] = i;
        }
    }

    GroupMemoryBarrierWithGroupSync();

    blobCount = blobCountAT.load();

    return { 0 };
}

Up at the top of this block, we define a few constants. WG_X and WG_Y describe the dimensions of our workgroup– we’re going to process blocks 8 pixels wide, and 4 pixels tall. These dimensions are chosen because most GPUs can execute 32 or 64 threads simultaneously. The maximum number of blobs we’ll add to the short list for each workgroup is set somewhat arbitrarily – we found 512 was a threshold that gave a good balance between performance and image quality.

You’ll also see that the coarseRasterize function takes an InitializedShortList parameter, but doesn’t appear to do anything with it. That’s because this implementation uses a set of sentinel struct types to enforce the correct ordering of the steps in the rasterization algorithm – essentially, this helps us catch bugs at compile time rather than runtime. It doesn’t affect how our gaussian splatting implementation works, so I won’t go deeper into it here.

Inside the function, the first thing that we do is to call GroupMemoryBarrierWithGroupSync. This is a memory barrier, which tells the GPU to wait here until all of the load and store operations being done by this workgroup on its shared memory have completed. This is important to avoid data races. The first barrier ensures that no threads start writing into the InitializedShortList parameter until the calling function has finished initializing it, while the barrier at the end of the function makes sure that all the threads have finished adding blobs to the list before the final count is retrieved with blobCount = blobCountAT.load();.

Then, we begin building our short list of relevant gaussian blobs. We want to split this work up across all of our workgroup threads, so that we can process the list of blobs efficiently and without duplicated work. The way we do this is that we ask each thread to start by accessing the blob in the global list that corresponds to its local thread index– an identifier that, similar to the texture coordinates we generated in the simpler example using SlangPy’s grid generator, allows each thread to understand where it sits within the workgroup. In this case, we’re using a 1-dimensional dispatch shape, and will need to do some math later to figure out what pixel we’re calculating within the image. I’ll explain that in more detail when we get there. Each thread will check its assigned first blob, and then skip ahead by the number of blobs that there are threads in the workgroup. So, with our WG_X (8) and WG_Y (4) describing a total thread group size of 32, we have threads examining blobs at that stride: Thread 0 checks blobs 0, 32, 64, … Thread 1 checks blobs 1, 33, 65, … And so on…

Whenever a blob is identified that intersects with the current tile, it’s added to the shortlist using this line:

        blobs[blobCountAT++] = i;

The shortlist blobs and its index incrementor blobCountAT didn’t appear in the excerpt above – that’s because they’re using workgroup shared memory, so they’re declared a bit differently, like this:

// ----- Shared memory declarations --------

// Note: In Slang, the 'groupshared' identifier is used to define
// workgroup-level shared memory. This is equivalent to '__shared__' in CUDA

// blobCountAT is used when storing blob IDs into the blobs buffer. It needs to be atomic
// since multiple threads will be in contention to increment it.
//
// Atomic<T> is the most portable way to express atomic operations. Slang supports basic
// operations like +, -, ++, etc.. on Atomic<T> types.
//
groupshared Atomic<uint> blobCountAT;

// This is used after the coarse rasterization step as a non-atomic
// location to store the blob count, since atomics are not necessary after the coarse
// rasterization step.
//
groupshared uint blobCount;

// The blobs buffer is used to store the indices of the blobs that intersect
// with the current tile.
//
groupshared uint blobs[GAUSSIANS_PER_BLOCK];

Using the groupshared identifier tells Slang that these variables need to be in the fast local memory available to all the threads in a workgroup. This shared memory space is much faster to access than global GPU memory, but it’s very limited in space– sometimes only on the order of tens of kilobytes.

Importantly, we declare the index incrementor, blobCountAT, to be atomic– this ensures that only one thread has access to read or write the variable at a time, preventing multiple threads from trying to simultaneously increment it.

After the threads in the workgroup finish iterating across the full list of blobs to identify the ones relevant to the current tile, we issue another GroupMemoryBarrierWithGroupSync to make sure all the threads in the workgroup finish, before finally writing out the final count of blobs in our shortlist to the non-atomic blobCount variable.

When coarseRasterize() completes, we have a list of just the gaussian blobs which affect the current tile, so we need not iterate through the entire list for each pixel. Because we’re no longer operating on the full list of gaussians, we can no longer assume that the list stays sorted in the back-to-front order needed for alpha blending. Because we built the short list in individual workgroup threads, we don’t know what order they were added to the list using blobs[blobCountAT++] = i;, so we will need to take an additional step for sorting them, which is done with bitonicSort, a sorting algorithm which makes similar use of workgroup shared memory to allow the workgroup threads to collaboratively sort the list.

Now that we have created a reduced list of gaussians to evaluate per-pixel, our rasterization could potentially be much faster! But you may have noticed that the maximum number of GAUSSIANS_PER_BLOCK is defined as 512– more than twice as many as the total list of gaussian blobs we used in our simplified example. Is that going to be a problem?

Differential Propagation and Intermediate Value Storage

There’s a second problem that was causing poor performance in our simplified example, but it’s less obvious, because it’s a byproduct of Slang doing derivative propagation for you.

Looking back at the simplified implementation, the differentiable function we used to calculate blob colors was simpleSplatBlobs():

/* simpleSplatBlobs() is a naive implementation of the computation of color for a pixel.
 * It will iterate over all of the Gaussians for each pixel, to determine their contributions
 * to the pixel color, so this will become prohibitively slow with a very small number of 
 * blobs, but it reduces the number of steps involved in determining the pixel color.
 */
 [Differentiable]
 float4 simpleSplatBlobs(GradInOutTensor<float, 1> blobsBuffer, uint2 pixelCoord, int2 texSize)
 {
    Blobs blobs = {blobsBuffer};

    float4 result = {0.0, 0.0, 0.0, 1.0};
    float4 blobColor = {0.0, 0.0, 0.0, 0.0};

    for (uint i = 0; i < SIMPLE_BLOBCOUNT; i++)
    {
        Gaussian2D gaussian = Gaussian2D.load(blobs, i);
        blobColor = gaussian.eval(pixelCoord * (1.0/texSize));
        
        result = alphaBlend(result, blobColor);
        if (result.a < 1.f / 255.f)
            continue;
    }

    // Blend with background
    return float4(result.rgb * (1.0 - result.a) + result.a, 1.0);
}

Because this function is differentiable, we need to be able to propagate its variables’ values through a chain of derivatives– that is, we need to know the value of result, blobColor, and gaussian at each step through the list of blobs, for every pixel we calculate. Storing all of that information is costly – especially because we’re doing these calculations on the GPU, and very little memory is available to us without significant latency in accessing it.

We can avoid needing to do all of this storage of intermediate values if, instead, we provide a way for Slang to recalculate the values as it progresses through the backward propagation. To do this, we provide a user-defined backwards form for part of our rasterization algorithm.

/*
 * fineRasterize() produces the per-pixel final color from a sorted list of blobs that overlap the current tile.
 *
 * The fine rasterizeration is where the calculation of the per-pixel color happens.
 * This uses the multiplicative alpha blending algorithm laid out in the original GS paper (https://repo-sam.inria.fr/fungraph/3d-gaussian-splatting/)
 * This is represented as a 'state transition' (transformPixelState) as we go through the blobs in order, so that we can
 * concisely represent the 'state undo' operation in the backwards pass.
 *
 * In Slang, custom derivative functions can be defined using the `[BackwardDerivative(custom_fn)]` attribute.
 */
[BackwardDerivative(fineRasterize_bwd)]
float4 fineRasterize(SortedShortList, Blobs blobset, uint localIdx, no_diff float2 uv)
{
    GroupMemoryBarrierWithGroupSync();

    PixelState pixelState = PixelState(float4(0, 0, 0, 1), 0);
    uint count = blobCount;
    // The forward rasterization
    for (uint i = 0; i < count; i++)
        pixelState = transformPixelState(pixelState, eval(blobset, blobs[i], uv, localIdx));

    maxCount[localIdx] = pixelState.finalCount;
    finalVal[localIdx] = pixelState.value;
    return pixelState.value;
}

/*
 * fineRasterize_bwd() is the user-provided backwards pass for the fine rasterization step.
 *
 * This is implemented as a custom derivative function because, while applying auto-diff directly to a function
 * with a loop can result in excessive state caching (a necessary part of standard automatic differentiation methods)
 *
 * For Gaussian splatting, there is a 'state undo' (undoPixelState) operation available. fineRasterize_bwd takes advantage of this
 * to recreate the states at each step of the forward pass instead of letting auto-diff store them.
 *
 * While it is important to represent the backwards loop explicitly in this way, the contents of the loop body (loading, evaluation,
 * blending, etc..) can still be differentiated automatically (and it would be tedious to do so manually).
 *
 * The loop body therefore invokes `bwd_diff` to backprop the derivatives via auto-diff.
 */
void fineRasterize_bwd(SortedShortList, Blobs blobset, uint localIdx, float2 uv, float4 dOut)
{
    GroupMemoryBarrierWithGroupSync();

    PixelState pixelState = { finalVal[localIdx], maxCount[localIdx] };

    PixelState.Differential dColor = { dOut };

    // The backwards pass manually performs an 'undo' to reproduce the state at each step.
    // The inner loop body still uses auto-diff, so the bulk of the computation is still
    // handled by the auto-diff engine.
    //
    for (uint _i = blobCount; _i > 0; _i--)
    {
        uint i = _i - 1;
        var blobID = blobs[i];
        var gval = eval(blobset, blobID, uv, localIdx);
        var prevState = undoPixelState(pixelState, i + 1, gval);

        var dpState = diffPair(prevState);
        var dpGVal = diffPair(gval);

        // Once we have the previous state, we can continue with the backpropagation via auto-diff within
        // the loop body. Note that the `bwd_diff` calls writeback the differentials to dpState and dpGVal,
        // and can be obtained via `getDifferential()` (or simply '.d')
        //
        bwd_diff(transformPixelState)(dpState, dpGVal, dColor);
        bwd_diff(eval)(blobset, blobID, uv, localIdx, dpGVal.getDifferential());

        pixelState = prevState;
        dColor = dpState.getDifferential();
    }
}

The first thing you’ll notice here is that, rather than simply being annotated as [Differentiable], our fineRasterize() function uses [BackwardDerivative(fineRasterize_bwd)] to indicate that, rather than Slang generating the backwards form of this function automatically, we instead want to provide the backward form of this function ourselves. Whereas before, we were storing the pixel state value for each iteration of the loop so that it could be replayed backwards, we now can use our domain-specific knowledge to reproduce the required value at each iteration instead.

Manually providing a backwards derivative form might seem like it defeats the purpose of using autodiff in Slang in the first place, but one of the very useful things about Slang is that it allows you to mix automatic and user-defined differentiation in a single propagation chain. That is, we can call fineRasterize() from within an automatically differentiated function (in this case, our top-level splatting function, splatBlobs()), provide a user-defined backwards form for just that function, and even invoke automatic differentiation on parts of that user-defined function using bwd_diff(). This way, we can get the benefits of avoiding that automatic caching of intermediate values during our pixel blending loop, but not have to take on all of the work of doing the derivatives for our full rasterization algorithm ourselves.

So, in the code above, the backward form of fineRasterize() loops backward over all of our blobs, evaluates each one, and performs an “undo” operation, which we define in undoPixelState.

/*
 * undoPixelState() reverses the alpha blending operation and restores the previous pixel
 * state.
 */
PixelState undoPixelState(PixelState nextState, uint index, float4 gval)
{
    if (index > nextState.finalCount)
        return { nextState.value, nextState.finalCount };

    return { undoAlphaBlend(nextState.value, gval), nextState.finalCount - 1 };
}

// …

/*
 * undoAlphaBlend() implements the reverse of the alpha blending algorithm.
 *
 * Takes a pixel value 'pixel' and the same 'gval' contribution &
 * computes the previous pixel value.
 *
 * This is a critical piece of the backwards pass.
 */
float4 undoAlphaBlend(float4 pixel, float4 gval)
{
    gval = preMult(gval);

    var oldPixelAlpha = pixel.a / (1 - gval.a);
    return float4(
        pixel.rgb - gval.rgb * oldPixelAlpha,
        oldPixelAlpha);
}

One thing to note about undoing an alpha blend: because alpha values are all within the range [0.0, 1.0], our undo is only possible if the pixel never becomes fully opaque. This is handled inside the transformPixelState function called by fineRasterize:

/*
 * transformPixelState() applies the alpha blending operation to the pixel state &
 * updates the counter accordingly.
 *
 * This state transition also stops further blending once the pixel is effectively opaque.
 * This is important to avoid the alpha becoming too low (or even 0), at which point
 * the blending is not reversible.
 *
 */
[Differentiable]
PixelState transformPixelState(PixelState pixel, float4 gval)
{
    var newState = alphaBlend(pixel.value, gval);

    if (pixel.value.a < 1.f / 255.f)
        return { pixel.value, pixel.finalCount };

    return { newState, pixel.finalCount + 1 };
}

Local Index Mapping

There’s one other notable difference between the simplified and full versions of this 2D gaussian splatter, which I mentioned above: the dispatch shape.

In the simplified version, we initiated the backward derivative propagation with this line of SlangPy:

module.perPixelLoss.bwds(per_pixel_loss,
                         spy.grid(shape=(input_image.width,input_image.height)),
                         blobs, input_image)

Recall that the spy.grid() function is a generator, which produces a grid-shaped set of IDs for the individual threads running the dispatched work.

By contrast, in this more complex version, we want to ensure that the coarseRasterize() and bitonicSort() functions can operate collaboratively on a set of pixels within a workgroup, so we create a mapping of pixels to thread IDs:

def calcCompressedDispatchIDs(x_max: int, y_max: int, wg_x: int, wg_y: int):
    local_x = np.arange(0, wg_x, dtype=np.uint32)
    local_y = np.arange(0, wg_y, dtype=np.uint32)
    local_xv, local_yv = np.meshgrid(local_x, local_y, indexing="ij")
    local_xyv = np.stack([local_xv, local_yv], axis=-1)
    local_xyv = np.tile(local_xyv.reshape(wg_x * wg_y, 2).astype(np.uint32),
                        ((x_max // wg_x) * (y_max // wg_y), 1))
    local_xyv = local_xyv.reshape((x_max * y_max, 2))

    group_x = np.arange(0, (x_max // wg_x), dtype=np.uint32)
    group_y = np.arange(0, (y_max // wg_y), dtype=np.uint32)
    group_xv, group_yv = np.meshgrid(group_x, group_y, indexing="ij")
    group_xyv = np.stack([group_xv, group_yv], axis=-1)
    group_xyv = np.tile(group_xyv[:, :, None, None, :], (1, 1, wg_y, wg_x, 1))
    group_xyv = group_xyv.reshape((x_max * y_max, 2)).astype(np.uint32)

    return ((group_xyv * np.array([wg_x, wg_y])[None, :] + local_xyv).astype(np.uint32))

What’s happening here is that we’re using some utility functions from NumPy to construct a grid of IDs manually, rather than asking SlangPy to generate it for us. We’re also providing the values in a single array, because, behind the scenes, SlangPy currently only supports a 1D dispatch shape– more general dispatch support is planned to be added soon. x_max and y_max represent the size of the full image, while wg_x and wg_y are the dimensions of the tile (and the workgroup that will calculate the pixel values within that tile). The IDs we create tell each thread both where it’s located within its workgroup, and which workgroup it belongs to within the full work dispatch, and from those, what pixel coordinates it’s responsible for calculating. We can then provide this set of IDs directly to our perPixelLoss function at dispatch:

module.perPixelLoss.bwds(per_pixel_loss, dispatch_ids, blobs, input_image)

Results

With these optimizations, we’re now able to operate on a much larger set of gaussian blobs. The full diff-splatting experiment uses 40960 blobs in total (and correspondingly defines their maximum size to be smaller, since we don’t need to cover as much ground with each blob). And even with this much larger number of blobs, overall execution is much faster. On the same system I used to generate the last post’s example image, all 10,000 iterations now take less than 3 minutes (compared to around 40 minutes for the simplified version). And as you can see, the image quality is orders of magnitude better.

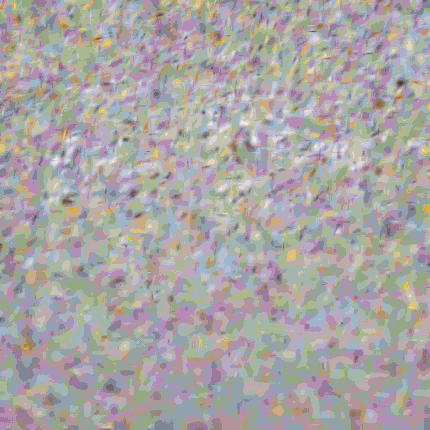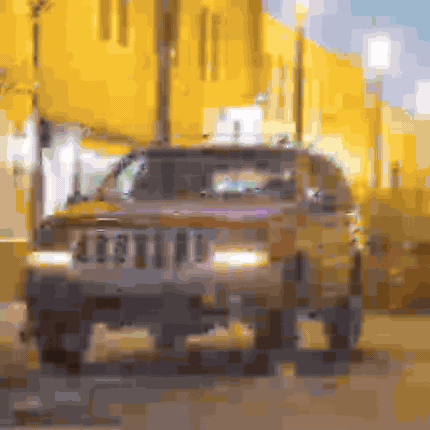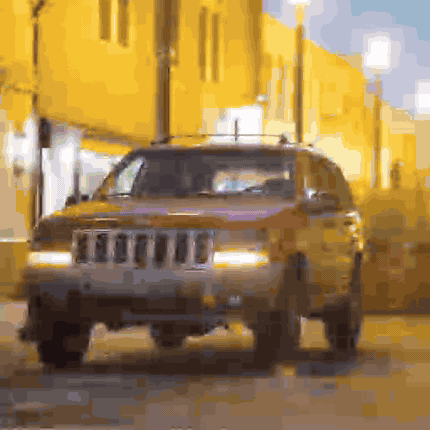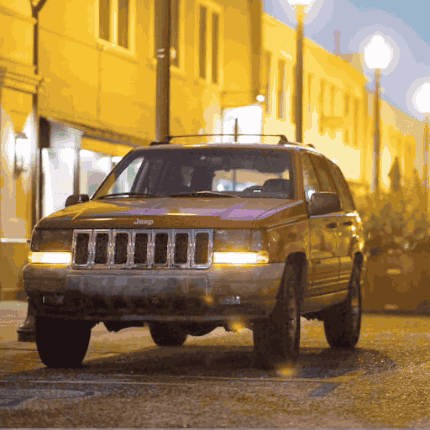
This optimization journey may feel familiar to graphics developers - we’ve applied many classic optimization patterns like tile-based processing, efficient memory management, and parallel workgroup coordination. The same patterns that have served graphics developers for years are equally crucial in neural graphics applications. The other part of our optimization equation is the mixing of automatic and user-defined differentiation, allowing us to use what we know about our color accumulation operation to avoid storage overhead, which is a particular strength of Slang. But whether you’re rendering traditional polygons or training neural representations, the underlying challenges of efficient hardware utilization remain remarkably similar.

You can start experimenting with the code for this 2D gaussian splatting example in a couple of ways: to try out the sample from SlangPy, check out the code in our SlangPy experiments set. If you want to try it out in your browser, head over to the Slang Playground, which uses the same Slang code in WebGPU.